电子轨道运动与动量矩解析
电子作轨道运动的动量矩
电子动量:MV是动量MVL乘以距圆心的距离L。s轨道的中心是原子核,p轨道与原子核有无关系?
原子核也是P轨道的对称中心,这是显而易见的。【玻尔的原子理论】丹麦物理学家玻尔运用经典运动定律和普朗克的量子概念,阐明了基于原子行星的原子结构初步理论。
模型。
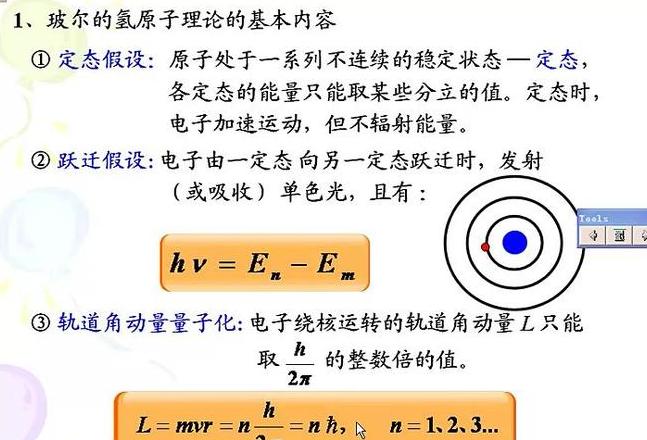
该理论的基础基于两个基本假设:(1)原子的电子不可能沿着经典理论允许的所有能量连续变化的轨道运动,但它们也不可能只沿着一组特殊的轨道运动。
只有当电子的动量等于h/2π的整数倍(h为普朗克常数)时,其轨道才稳定。
在每个稳定轨道上,原子都具有一定的能量。
稳定状态的电子既不吸收也不发射辐射。
(2) 当电子从一种静止状态移动到另一种静止状态时,会发生辐射的吸收或发射。
当原子从一个能级的能量En运动到另一个能级的能量Em时,它会发射或吸收一定频率的光。
频率的数值是玻尔理论只考虑了电子的圆形轨道。
也就是说,电子只有一个自由度,这解释了只有一个电子的氢原子和类氢原子的谱线频率。
该理论在具有两个或多个电子的原子发射的光谱方面遇到了根本性的困难。
后来,索末菲推广了玻尔的量子化条件,使其不仅可以解释氢原子的光谱,而且可以更好地解释具有单价电子的复杂原子的光谱。
玻尔理论的部分成果促进了量子理论的发展,在历史上发挥了重大作用。
[玻尔轨道] 在玻尔理论中,电子被认为以许多离散的圆形轨道绕原子核运行。
轨道半径约为10至8厘米。
在不同轨道上循环的电子各自具有一定的能量。
当电子从外轨道移动到内轨道时,它会发射光子。
电子沿轨道运动的概念并不正确,现已被量子力学的概率分布概念所取代。
然而,由于其直观的性质,轨道谓词仍然经常被用来近似描述原子内电子运动的规律性。
根据玻尔量子化条件,对于圆形轨道,可以计算出轨道半径,电子的运动力矩P为P=mvr,根据电子与原子核之间的作用力为库仑力,所以有。
圆形轨道的向心力是量子数(参见条目玻尔原子理论)。
我们得到最接近原子核的圆形轨道的半径,约为 0.529 × 10-8 [cm]。
它在原子物理学中常用作为a0表示的长度单位:我希望这对你有用!